Vamos a comentar intuitivamente uno de los algoritmos más famosos y más útiles de la geometría computacional usando un ejemplo práctico. Aprenderemos a generar imágenes como esta:
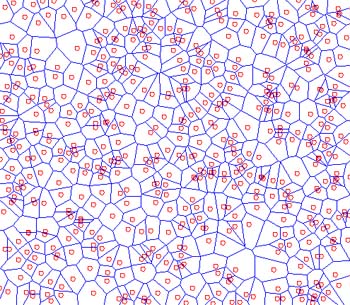
Comenzamos la aventura. Imaginaros que tenemos una empresa de transporte con varias centrales de distribución, cada punto de la imágen representa uno de estos centros:

Ahora imaginaros que debemos determinar las zona que debe cubrir cada central de distribución de forma que tengamos que viajar lo mínimo posible. Es decir, debemos determinar las zonas del plano que están más cercanas a cada punto.
Para calcular estas zonas hay que seguir una serie de pasos. Primero debemos aplicar el algoritmo de Delaunay, que consiste en trazar triángulos entre los vértices con ciertas restricciones que ahora veremos. Veamos una posible triangulación:
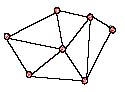
Esta es una forma de triangular, pero para nuestro propósito no es válida. Debemos conseguir una triangulación de forma que Cualquier circunferencia trazada entre los 3 vértices de cada triángulo no tenga ningún otro punto dentro. Lo veremos más claro con una imágen que demuestra que la triangulación anterior no era válida:
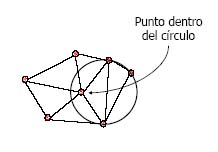
¿Cómo solucionamos el problema? Pues probando diversas triangulaciones (Hay un método complicado de explicar que lo hace muy bien) hasta que no haya ninguna circunferencia que toque más de 3 vértices. En nuestro caso solo tenemos que cambiar una arista:
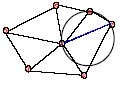
Fijaros que hemos cambiado un poco la triangulación y ahora al trazar la circunferencia ya no tenemos ningún otro vértice interior. Si hacemos lo mismo con el resto de triángulos vemos que hemos conseguido que no tengan otros vértices dentro, en este momento hemos conseguido la Triangulación de Delaunay a partir de los vértices/centrales de distribución iniciales. En la siguiente imagen trazamos todas las circunferencias posibles, fijaros que ninguna toca más de 3 vértices.
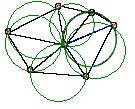
Pufff, un poco lioso pero lo que queda es cuesta abajo. A continuación debemos calcular las regiones más cercanas a cada punto (A estas regiones las llamaremos Regiones de Voronoi). Para ello nos apoyaremos en la Triangulación de Delaunay que ya hemos calculado. Marcamos el punto central de cada circunferencia y trazamos Perpendiculares a las aristas de los triángulos. Vamos a verlo con dos de los círculos para no liar (Los puntos amarillos son los centros de las circunferencias y las líneas naranjas son perpendiculares a las aristas de los triángulos):

Si seguimos aplicando el mismo método (y eliminamos del dibujo los circulos para no liar) obtendremos lo siguiente:
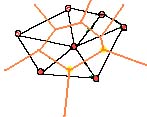
Si además eliminamos la Triangulación de Delaunay, tendremos la imagen definitiva donde se definen las zonas más cercanas a cada centro de distribución:
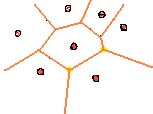
Por ejemplo, la zona coloreada de verde es la Región de Voronoi del punto A. Esto quiere decir que todo lo que está pintado de verde está más cerca de A que de cualquier otro punto del dibujo. Lo podéis comprobar con una regla si no os convenzo 😉
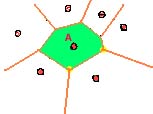
Si habéis llegado hasta aquí, tenéis premio: Un applet donde haciendo clicks podéis ir colocando las sedes de vuestra empresa y vais viendo en tiempo real la triangulación de Delaunay y las regiones de Voronoi. También podéis generar muchos puntos dándole al botón Generar, con el que conseguiréis una imagen similar a la mostrada al inicio de este artículo. A los programadores os pongo el código fuente por si quieren trastear algo, os aviso que está muy poco documentado.
Resumiendo, en geometría computacional las regiones de Voronoi son las zonas del plano más cercanas a un conjunto dado de puntos. Esto a nivel práctico lo utilizan muchas empresas para definir sus zonas de cobertura. Por ejemplo, McDonalds lo utiliza para decidir donde tiene que poner una nueva sede. También se utiliza en planes de prevención de riesgos para saber a que zonas afectaría un escape de una central nuclear.
También se utiliza en aplicaciones más artísticas, como en la primera imágen de este artículo, la creación de cristaleras etc. También podéis generar vuestras regiones de voronoi utilizando Photoshop: Filtro -> Textura ->Vidriera . Para aplicar ese filtro Photoshop internamente realizar la Triangulación de Delaunay que hemos aprendido y posteriormente calcula las Regiones de Voronoi. Todos a crear Vidrieras y si no os queda algo claro preguntad 🙂






